Второе: скорости двух тел равны, если пространства, проходимые ими, пропорциональны времени прохождения.
Второе определение является обобщением первого, первое вытекает из второго и должно быть справедливым, если справедливо второе.
Вооруженный этими двумя определениями, Галилей приступает к сравнению конкретных случаев падения тел. Пусть по СВ и СА падают два одинаковых тела:
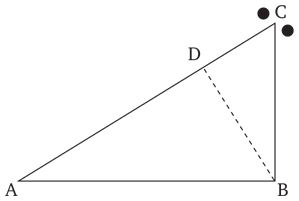
Рис. 4
Скорость тела, падающего по СВ, будет больше скорости тела, падающего по СА. Действительно, в течение того времени, в которое первое падающее тело пройдет всю СВ, второе пройдет на СА часть CD, которая будет меньше СВ. Отсюда мы можем сделать вывод, что тело движется с большей скоростью по вертикали, чем по наклонной, и кроме того, в соответствии с первым определением, – что скорости тел, падающих по наклонной и по вертикали, не равны.
Но если мы возьмем отношение времен падения по всей наклонной и всей вертикали, то оно окажется равным отношению длин наклонной и вертикали. Отсюда, в соответствии со вторым определением, мы можем сделать вывод, что скорости тел, падающих по наклонной и по вертикали, равны.
Таким образом, следуя рассуждению Галилея, мы получили два противоречащих суждения:
«Скорости тел, падающих по СА и СВ, равны».
«Скорости тел, падающих по СА и СВ, не равны».
Противоречие налицо. Что же делать? Выбросить одно из противоречащих положений? Но они оба справедливы. Выбросить одно из определений равенства скоростей? Но они тоже оба справедливы. В чем же дело?