Доказательство бесконечной делимости времени заключается в указании операции, с помощью которой можно провести это деление. «Так всякое движение происходит во времени, и во всякое время может происходить движение, и так как, далее, все движущееся может двигаться быстрее и медленнее, то во всякое время будет происходить и более быстрое и более медленное движение. Если же это так, то и время должно быть непрерывным. Я разумею под непрерывным то, что делимо на всегда делимые части; при таком предположении время должно быть непрерывным» [Физика, 232b21—27]. Далее Аристотель пишет: возьмем два тела – А и В; пусть А – более скорое тело, а В – более медленное, которое проходит расстояние ΓΔ за время ΖΗ61:
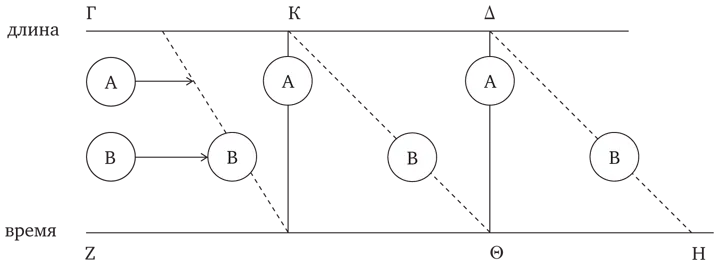
Рис. 3
Более скорое тело А пройдет то же расстояние ΓΔ за меньшее время ΖΘ. За время ΖΘ более медленное тело В пройдет отрезок ΓΚ, а более скорое тело А пройдет этот же отрезок за меньшее время и т. д., и т. д. «И всегда будет проходить так, если переходить от более быстрого к более медленному, и от более медленного к более быстрому, пользуясь указанным доказательством, ибо более быстрое будет делить время, а более медленное – длину» [Физика, 232b28—233а8].
Кроме того, он показал, что если мы берем от движения часть, то соответственно берутся части от пути и времени, то есть каждой части движения соответствует своя пропорциональная часть пути и времени, которую можно соответственно измерить.
Тем самым уточнялась связь между движением, пространством и временем и обосновывалась возможность измерять движение, измерять путь и время.