Связь абстракции бесконечного с процессами измерения, последовательного деления и счета явственно выступает впервые у Зенона, философа элеатской школы. В своей апории «дихотомия» он показал процесс деления, который никогда не может быть доведен до конца. Сущность его рассуждения заключается в следующем. Пусть необходимо пройти отрезок АВ=а. Но очевидно, что, прежде чем пройти АВ, надо пройти половину его АВ1=a/2. Но прежде чем пройти АВ1, надо пройти половину его АВ2=а/4 и т. д., и т. д.:
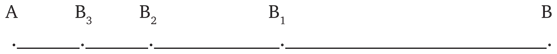
Рис. 1
Таким образом, получается бесконечное количество отрезков, которое надо было пройти за конечный промежуток времени, а это казалось Зенону невозможным. Нам здесь важен тот момент, что процессы повторного деления привели Зенона к необходимости ввести если не формально, то, во всяком случае, по существу абстракции «бесконечно большого» количества и «бесконечно малой» величины. «Зенон доказывает, что если существует множественное, то оно и велико и мало; оно настолько велико, что множественное бесконечно по своему количеству. ‹…› Оно так мало, что не имеет величины» (Симплиций)52. Но в этих абстракциях, в самом их названии уже заложены противоречия. Что может означать, например, абстракция «бесконечно малая величина»? Абстракция величины предполагает определенные границы, «бесконечное» эти границы отрицает. Что же остается? Величина, не имеющая никакой величины. Зенон прекрасно осознает, что это противоречие, и исходя из него отрицает возможность существования как бесконечно больших, так и бесконечно малых: «Он показывает, что того, что не имеет ни величины, ни толщины, ни массы, не существует. Ибо если бы мы его прибавили к другому, оно не увеличило бы последнего; если именно оно не имеет величины и прибавляется к другому, оно ничего не может присовокупить к величине этого другого и, таким образом, то, что прибавляется, есть ничто. Точно так же, если его отнимут от другого, последнее вследствие этого не уменьшится; оно, следовательно, есть ничто» [Гегель, 1932, IX, с. 233–234].