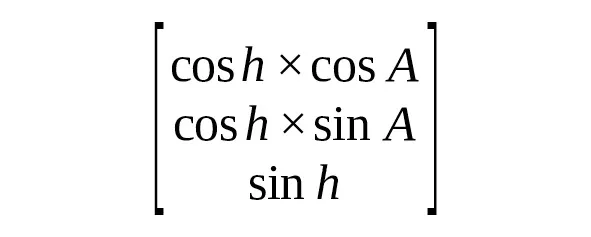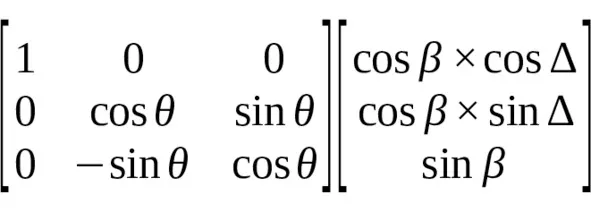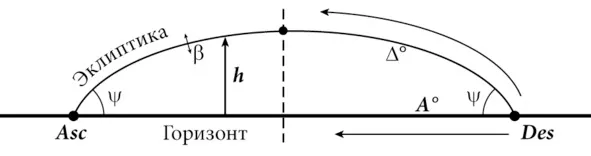
Рис. 4. Плоскости Горизонта и эклиптики в проекции Меркатора. Горизонт представлен, как прямая линия (осевой срез проекции), а Эклиптика – соответственно дугой. На чертеже введены следующие обозначения: h – высота над горизонтом; A – угол, отсчитываемый в плоскости горизонта, от Десцендента, влево (на восток, по ходу зодиака);∆ – будет углом, в плоскости Эклиптики, отсчитываемым от ДЕСЦЕНДЕНТА по ходу зодиака; β – эклиптическая широта данной точки (выше/ниже от Эклиптики).
Остаётся выяснить: как найти точку эклиптики, которая будет выше всего над горизонтом?!
А это сделать элементарно. Есть две плоскости: они пересекаются вдоль некоторой оси под определённым углом. Разумеется, угол наклона эклиптики к горизонту непрерывно меняется. Но пусть в некий, выбранный нами момент времени t0 он будет равен некоторому значению θ. Две данные плоскости тогда можно математически связать, через сферическую систему координат единичного радиуса, следующим образом:
=