Две параллельные прямые.
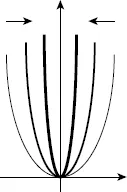
Если мы рассмотрим четную (делится на 2) степенную функцию, которая имеет следующую общую формулу: у = kx2n + b, то ее графиками будут параболы, которые с увеличением показателя степени своими ветвями все более и более приблизятся к вертикальной оси координат, стремясь превратиться в две полупрямые, параллельные вертикальной оси.
Если мы сравним общее уравнение, задающее параболы, с общим уравнением прямых линий, то увидим их внешнее сходство.
Y = kx2n + b – уравнение парабол, у = kx + b – уравнение прямых.
Если мы вспомним известную из школьного курса алгебры формулу «разницы квадратов»: а2 – b2 = (a-b)(a+b) – и применим ее в приложении к некоторым уравнениям парабол: у = х2 + b2, то мы увидим связь между параболами и прямыми: у = х2 + b2 = (x-b)(x+b). Как вы сами можете видеть, в данной формуле имеется уравнение параболы у = х2 + b2 и уравнения прямых у = х – b и у = х + b, которые указывают на тот факт, что при вырождении параболы переходят в параллельные или совпадающие прямые (как мы это видели, говоря о повышении степени в уравнении парабол).
Мы рассмотрели все возможные случаи, которые могут быть получены на основе эллипса. Включая сам эллипс, мы получили шесть возможных вариантов, которые позволят нам рассмотреть шесть различных моделей объектов и субъектов (наблюдателей) мира, которые будут создавать гармоничные пары «объект – субъект», которые помогут нам понять возможные варианты отношений человека с окружающим миром.
Модель «эллипс»
Особенности объекта. Доступен для изучения; имеется возможность определить основные параметры; известна или понятна конечная цель исследования объекта (процесса, теории и т. д.).
Особенности субъекта. Он создатель своего мира, в котором все ясно и понятно, в котором только «свои», все те, кто его понимают и принимают его мир. Он конструктор, изобретатель, автор совершенной, логической модели, которая, по его убеждению, максимально совпадает с идеальной эллиптической моделью объекта исследования.