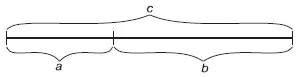
Рис. 1.7. Так можно изобразить золотую пропорцию
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если с принять за 1, а = 0,382.
Стоит обратить внимание на загадочные величины 0,618 и 0,382. Эти коэффициенты последовательности Фибоначчи чрезвычайно интересны. На этой пропорции базируются основные геометрические фигуры.
Прямоугольник с таким соотношением сторон стали называть золотым прямоугольником: если от него последовательно и до бесконечности отрезать квадрат, то всегда останется золотой прямоугольник.
Существует еще золотой треугольник, у которого отношение длины боковой стороны к длине основания равняется 1,618, а также золотой кубоид.
В совершенной пентаграмме – пятиконечной звезде – каждая из составляющих ее пяти линий делит другую в золотой пропорции, а концы звезды образуют золотые треугольники.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.